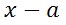Teorema del factor, División sintética y Regla de signos de Descartes

Teorema del factor

Este teorema dice que:

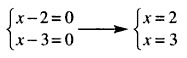
Un número real "a" es raíz de un polinomio p(x) si y sólo si p(x) es divisible por (x – a)

     Luego de haber leído la publicación anterior se puede observar que el teorema del factor es una consecuencia directa del teorema del resto. Ya  que para que un polinomio p(x) sea divisible por otro de la forma (x - a) el resto de la división de p(x) entre (x - a) debe ser igual a cero. Lo cual se puede conocer facilmente aplicando el teorema del resto a dicho polinomio  y verificando si el resto es o no igual a cero.

     Retomando el ejemplo de la publicación anterior se tiene que al dividir:

 entre 

     

     El resto, obtenido mediante el teorema del resto, es igual a:

     

     Por lo que, de acuerdo a lo enunciado en el teorema del factor, -1 es raiz de p(y) ya que el resto de la división anterior es cero. Confirmándose además que y + 1 es divisor de p(y). De modo que del teorema del factor pueden sacarse las siguientes aseveraciones: 

Un número real "a" es raíz de un polinomio p(x) si y sólo si p(a) = 0

Y también puede decirse que: 

un polinomio de la forma (x – a) es un factor de un polinomio p(x)

si y sólo si p(a) = 0

Fuentes:

• Métodos Numéricos Con Matlab. Alicia Cordero Barbero. Ed. Univ. Politéc. Valencia, 2005. Pag. 48 de 493.
• Matemática Para el Ingreso. Universidad Nac. del Litoral. Pag 127.
• Teorema del resto en Wikipedia.

_________________________________________________________________________________

División sintética

    Un método rápido alternativo a la división larga es la división sintética, la cual sirve únicamente para dividir un polinomio de grado 1 o mayor entre otro polinomio que este en la forma (x – c), donde c es una constante.

     En la división sintética se escriben sólo las partes esenciales de la división larga. A continuación se muestra una comparación entre la división larga y la división sintética en la que se divideentre

     Se puede observar que en la división sintética se escriben sólo los coeficientes del dividendo (los 4 numeros que se encuentran a la derecha del 3) poniendo un cero en aquellos lugares donde falte una potencia de x. Y en lugar de x - 3 se escribe simplemente 3, sin signo negativo, ya que el ponerlo como positivo permite sumar en lugar de restar, y ésto hace que se cambie el signo de los coeficientes del renglón de en medio de la división sintética (6, -3 y -9) con respecto a su contraparte en la división larga. A continuación se muestra el proceso mediante el cual se efectuó la división sintética.

     Se comienza por escribir los coeficientes apropiados para representar el divisor y el dividendo.

     Se baja el 2, se multiplica (3)(2) = 6, y se escribe el resultado en el renglón de en medio. Luego se suma: 

     Se repite el proceso de multiplicar y luego sumar hasta completar la tabla.

     De la última línea de la división sintética, se puede observar que el cociente es  y el residuo es - 4. Por consiguiente:

Fuente:

• Matemáticas para el Cálculo. 5ta Edición. James Stewart, Lothar Redlin. Cengage Learning Editores, 2007. Pag. 267 de 1056.

_________________________________________________________________________________

Regla de signos de Descartes

     Esta regla permite determinar el número máximo posible de raíces reales positivas y negativas de una ecuación polinómica determinada. esta regla dice que:

Sea p(x) un polinomio con coeficientes reales tal que p(0) sea diferente de 0. Entonces:

• El número de raíces reales positivas de p(x) es igual al número de variaciones de signos en la sucesión numérica formada por sus coeficientes, o menor que esa cantidad en un múltiplo de 2.

• El número de raíces reales negativas de p(x) es igual al número de  variaciones de signos en la sucesión numérica formada por sus coeficientes pero en p(-x), o menor que esa cantidad en un múltiplo de 2.

     Hay que recordar que este teorema habla de las raíces reales de p(x), y que para aplicar correctamente el teorema, p(x) debe estar escrito en forma estandar o canónica, es decir, de la potencia mayor a la menor.

     Al entender esta regla se debe tener en cuenta el siguiente término. Por "variaciones de signos" de los coeficientes reales de un polinomio, se da a entender que dos coeficientes consecutivos tienen signos opuestos. Así por ejemplo, si se tiene el polinomio, y teniendo en cuenta que los términos con coeficiente cero son positivos, la secuencia de los signos es:

     Por lo que hay 2 variaciones de signo, tal como lo indican las flechas, por lo tanto hay "a lo mucho" 2 raíces positivas (lo que no quiere decir que tenga que haberlas efectivamente). Para conocer las raíces negativas se utiliza p(-x) de modo que primero se sustituyen todas las x por - x en el polinomio:

     Y por consecuente, la secuencia de los signos ahora es:

     Donde según las flechas hay 3 variaciones de signo, por lo que hay "a lo mucho" 3 raíces negativas (lo que igualmente no quiere decir que las haya efectivamente).

     Como ha podido apreciarse, esta regla sólo ofrece conjeturas, sin una seguridad definitiva, sobre la naturaleza de las raíces de un polinomio p(x). De cualquier forma es interesante conocer estas posibilidades sobre las raíces a manera de guía en el trabajo.

Fuentes:

• Álgebra y trigonometría con geometría analítica. Arthur Goodman, Lewis Hirsch. Pearson Educación, 1996. Pag. 284 de 642.
• Algebra superior, Volumen 1. Kreemly Pérez Lluberes, María Altagracia López Ferreira. INTEC, 1984. Pag. 290 de 406.

Teorema fundamental del álgebra, Método de Ruffini y Teorema del resto

Teorema fundamental del álgebra

     Este teorema fué demostrado por Karl Friedrich Gauss (1777 – 1855) a la edad de 22 años como parte de su tésis doctoral en 1799. El teorema debe su nombre a su importancia y utilidad. El teorema enuncia que:

Si p(x) es un polinomio de grado n > 0 cuyos coeficientes son números complejos, entonces la ecuación p(x) = 0 tiene al menos una raíz en el sistema de números complejos.

     Recordando que, como los números reales son también números complejos, un polinomio con coeficientes reales también satisface este teorema. Como recordatorio, la raíz de un polinomio es un número tal que hace que el polinomio valga cero, es decir, que cuando resolvemos un polinomio a cero, sus soluciones son las raíces del polinomio.

Fuente:

• Álgebra y trigonometría con geometría analítica. Arthur Goodman, Lewis Hirsch. Pearson Educación, 1996. Pag. 274 de 642.

_________________________________________________________________________________

Método de Ruffini

     El método, o algoritmo, de Ruffini es un método para hallar las soluciones de ecuaciones de cualquier orden, con la condición de que sus soluciones sean enteras. Para soluciones fraccionarias este método resulta bastante difícil.

     Además, este algoritmo sirve para factorizar ecuaciones o expresiones matemáticas. Se muestra a continuación un ejemplo que explica este método. Hallar las soluciones de la siguiente ecuación de 2do grado:

     Primeramente se sitúan los coeficientes de la ecuación (1), (-5) y (6) ordenados en potencias de (x) decrecientes, de modo que quedan de la siguiente forma:

     Donde n es una constante, elegida a azar entre los divisores del último coeficiente (6). Estos divisores son llamados valores de prueba, y para este ejemplo dichos valores son:

     El método consiste en elegir, al azar, un valor de prueba de entre los anteriores, colocarlo en lugar de n, e ir sumando y multiplicando estos valores de la forma que se mostrará a continuación, de manera que al final se obtenga un (-6), que sumado al último valor (es decir el 6 de la última columna) nos de (0). Ésto se muestra en la siguiente imagen. Como dato extra, ese último valor del polinomio, osea el 6, es llamado el término independiente del polinomio, y es el termino del polinomio que no esta multiplicando a ninguna variable.

     Eligiendo, aleatoriamente, como primer valor de prueba al numero (3), éste se sitúa en el lugar de n. Entonces, se baja el primer coeficiente, osea el (1), como se muestra a continuación:

     Seguidamente se multiplica dicho primer coeficiente (en esta caso el 1) por el valor de prueba (3) y el resultado se sitúa abajo del coeficiente de la segundo columna. Luego, dicho resultado se suma con el coeficiente que tiene encima de el (osea el -5) y el nuevo resultado (-2) se pone hasta abajo de esa columna (osea abajo del 3) tal como se aprecia en la figura anterior.

     A continuación se repite la operación con el siguiente valor, es decir con el (-2), el cual se multiplica por el valor de prueba (3), dando como resultado un (-6) que se pone debajo del coeficiente de la siguiente columna (osea abajo del 6), para a continuación sumárselo al último valor (6), y con esto obtener en (0), este procedimiento se muestra en la siguiente figura:

     Como se obtuvo un (0), esto indica que el algoritmo de Ruffini ha resultado  correcto, significando que el valor de 3 es una solución de la ecuación, y que los valores resultantes de la última fila (la fila de hasta abajo) son los coeficientes de una ecuación  de un grado menor al del enunciado, esto es:

     De esta forma se puede escribir la ecuación factorizada:

     De donde las soluciones serán:

Nota 1: los valores de prueba que resulten soluciones de la ecuación, pueden ser usados en cualquier orden. Así en la ecuación que hemos hallado, probamos en primer lugar el valor (2), que sabeos que es una solución de la ecuación. Asi nos queda:

Nota 2: si se usa un valor de prueba que no es solución de la ecuación, no se obtendrá un cero en la última posición (debajo de última columna). Asi, en el ejemplo anterior podemos probar el (1), que aunque es divisor del número 6, no es una solución de la ecuación. Ésto se comprueba:

 Nota 3: el algoritmo de Ruffini puede ser aplicado tantas veces como sea necesario.

Fuente:

• La matemática es fácil: Manual de matemática básica para gente de letras. José Manuel Casteleiro Villalba. ESIC Editorial, 2008. Pag. 229 de   462.

_________________________________________________________________________________

Teorema del Resto

     Se sabe que si al dividir un polinomio p(x) por otro q(x) el resto, o residuo, es cero se puede decir que p(x) es divisible por q(x), o que q(x) es divisor de p(x), o bien que p(x) es múltiplo de q(x).

     En ocasiones solo nos interesa saber si un polinomio es divisor de otro, y no tanto conocer el resultado de la división. Si se pudiera calcular directamente el resto de la división, seria fácil responder rápidamente si un polinomio es divisible por otro o no. Y precisamente el teorema del resto es un método que nos permite calcular lo anterior, pero sólo es posible utilizarlo cuando el divisor es de la forma (x + a), (x - 3), (x - 1/5)..., es decir, solamente cuando tiene la forma (x – a). El teorema en cuestión se enuncia que:

Sea "a" un número real y p(x) un polinomio de grado n > 0, el resto de la división de p(x) por (x – a) es: resto = p(a).

     Cabe señalar que, debido a que valen las propiedades asociativa y conmutativa, se puede afirmar que:

"Si  p (x)  =  q (x)  entonces  p (a)  =  q (a)  para todo "a" que pertenezca al conjunto de los números Reales"

     Cabe también aclarar que para llevar acabo este procedimiento de manera correcta el signo que tenga "a" debe ser cambiado al momento de calcular el polinomio p(a). Es decir que si por ejemplo un polinomio p(x) se va a dividir entre x + 7 , el +7 se tiene que cambiar al signo contrario de forma que el polinomio se calcule como p(-7). 

     Para demostrar que el resto = p(a), no queda otra alternativa que calcular p(a). A continuación se muestra un ejemplo para demostrar el teorema.

     ¿Es  divisible por  ?

     Como  tiene la forma  entonces:

     

     por lo tanto: 

Fuentes:

• Matemática Para el Ingreso. Universidad Nac. del Litoral. Pag 125.
• Video explicativo del teorema del resto en youtube.