Teorema fundamental del álgebra
Este teorema fué demostrado por Karl Friedrich Gauss (1777 – 1855) a la edad de 22 años como parte de su tésis doctoral en 1799. El teorema debe su nombre a su importancia y utilidad. El teorema enuncia que:
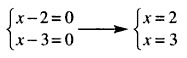
Si p(x) es un polinomio de grado n > 0 cuyos coeficientes son números complejos, entonces la ecuación p(x) = 0 tiene al menos una raíz en el sistema de números complejos.
Recordando que, como los números reales son también números complejos, un polinomio con coeficientes reales también satisface este teorema. Como recordatorio, la raíz de un polinomio es un número tal que hace que el polinomio valga cero, es decir, que cuando resolvemos un polinomio a cero, sus soluciones son las raíces del polinomio.
Fuente:
- Álgebra y trigonometría con geometría analítica. Arthur Goodman, Lewis Hirsch. Pearson Educación, 1996. Pag. 274 de 642.
_________________________________________________________________________________Método de Ruffini
El método, o algoritmo, de Ruffini es un método para hallar las soluciones de ecuaciones de cualquier orden, con la condición de que sus soluciones sean enteras. Para soluciones fraccionarias este método resulta bastante difícil.
Además, este algoritmo sirve para factorizar ecuaciones o expresiones matemáticas. Se muestra a continuación un ejemplo que explica este método. Hallar las soluciones de la siguiente ecuación de 2do grado:
Primeramente se sitúan los coeficientes de la ecuación (1), (-5) y (6) ordenados en potencias de (x) decrecientes, de modo que quedan de la siguiente forma:
Donde n es una constante, elegida a azar entre los divisores del último coeficiente (6). Estos divisores son llamados valores de prueba, y para este ejemplo dichos valores son:
El método consiste en elegir, al azar, un valor de prueba de entre los anteriores, colocarlo en lugar de n, e ir sumando y multiplicando estos valores de la forma que se mostrará a continuación, de manera que al final se obtenga un (-6), que sumado al último valor (es decir el 6 de la última columna) nos de (0). Ésto se muestra en la siguiente imagen. Como dato extra, ese último valor del polinomio, osea el 6, es llamado el término independiente del polinomio, y es el termino del polinomio que no esta multiplicando a ninguna variable.
Eligiendo, aleatoriamente, como primer valor de prueba al numero (3), éste se sitúa en el lugar de n. Entonces, se baja el primer coeficiente, osea el (1), como se muestra a continuación:
Seguidamente se multiplica dicho primer coeficiente (en esta caso el 1) por el valor de prueba (3) y el resultado se sitúa abajo del coeficiente de la segundo columna. Luego, dicho resultado se suma con el coeficiente que tiene encima de el (osea el -5) y el nuevo resultado (-2) se pone hasta abajo de esa columna (osea abajo del 3) tal como se aprecia en la figura anterior.
A continuación se repite la operación con el siguiente valor, es decir con el (-2), el cual se multiplica por el valor de prueba (3), dando como resultado un (-6) que se pone debajo del coeficiente de la siguiente columna (osea abajo del 6), para a continuación sumárselo al último valor (6), y con esto obtener en (0), este procedimiento se muestra en la siguiente figura:
Como se obtuvo un (0), esto indica que el algoritmo de Ruffini ha resultado correcto, significando que el valor de 3 es una solución de la ecuación, y que los valores resultantes de la última fila (la fila de hasta abajo) son los coeficientes de una ecuación de un grado menor al del enunciado, esto es:
De esta forma se puede escribir la ecuación factorizada:
De donde las soluciones serán:
Nota 1: los valores de prueba que resulten soluciones de la ecuación, pueden ser usados en cualquier orden. Así en la ecuación que hemos hallado, probamos en primer lugar el valor (2), que sabeos que es una solución de la ecuación. Asi nos queda:
Nota 2: si se usa un valor de prueba que no es solución de la ecuación, no se obtendrá un cero en la última posición (debajo de última columna). Asi, en el ejemplo anterior podemos probar el (1), que aunque es divisor del número 6, no es una solución de la ecuación. Ésto se comprueba:
Nota 3: el algoritmo de Ruffini puede ser aplicado tantas veces como sea necesario.
Fuente:
- La matemática es fácil: Manual de matemática básica para gente de letras. José Manuel Casteleiro Villalba. ESIC Editorial, 2008. Pag. 229 de 462.
_________________________________________________________________________________
Teorema del Resto
Se sabe que si al dividir un polinomio p(x) por otro q(x) el resto, o residuo, es cero se puede decir que p(x) es divisible por q(x), o que q(x) es divisor de p(x), o bien que p(x) es múltiplo de q(x).
En ocasiones solo nos interesa saber si un polinomio es divisor de otro, y no tanto conocer el resultado de la división. Si se pudiera calcular directamente el resto de la división, seria fácil responder rápidamente si un polinomio es divisible por otro o no. Y precisamente el teorema del resto es un método que nos permite calcular lo anterior, pero sólo es posible utilizarlo cuando el divisor es de la forma (x + a), (x - 3), (x - 1/5)..., es decir, solamente cuando tiene la forma (x – a). El teorema en cuestión se enuncia que:
Sea "a" un número real y p(x) un polinomio de grado n > 0, el resto de la división de p(x) por (x – a) es: resto = p(a).
Cabe señalar que, debido a que valen las propiedades asociativa y conmutativa, se puede afirmar que:
"Si p (x) = q (x) entonces p (a) = q (a) para todo "a" que pertenezca al conjunto de los números Reales"












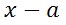


Caesars Palace Casino and Hotel - Mapyro
ResponderEliminarFind 양주 출장안마 the best price for the Caesars Palace Casino and Hotel in Macau. See 경기도 출장안마 19 photos and read 30 구미 출장안마 tips and reviews. "We have the best prices 안양 출장샵 for a hotel. 제천 출장샵 "